解けそうで解けない？！
数学パズルで、頭の体操をしてみませんか？
忙しい日々の、ちょっとした気分転換にもおすすめです。
嘘つきパズル！この中に嘘つきは何人いる？！
問題
森の中で、10人の妖精が手をつなぎ、輪になって踊っています。
10人の妖精の中には、正直でやさしいフェアリーと、嘘つきでいたずらっ子のピクシーが混ざっていますが、見た目では区別がつきません。
「あなたが手を繋いでいる相手は、ピクシーですか、それともフェアリーですか？」
と聞くと、10人全員が「ピクシーだ」と答えました。
質問に、フェアリーは必ず正直に、ピクシーは必ず嘘で答えるとすると、この中にピクシーは何人いますか？
ヒントが知りたい方は下に！
ヒント
10人のうち1人をフェアリー（ピクシーでも可）と仮定して図に書いてみよう！
輪になった10人の妖精をA～Jとします。
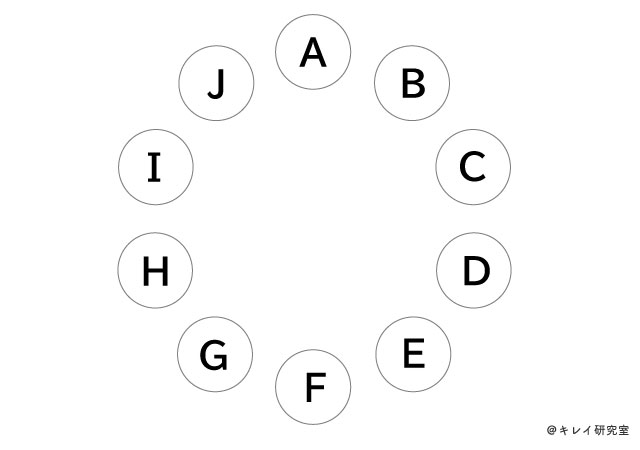
ヒントにもある通り、10人（A～J）のうち1人をフェアリーだと仮定してみましょう。
ここから答えを導き出せるかな？
答えは解説の下にあります！
解説
輪になった10人の妖精をA～Jとします。
ヒントにもある通り、10人（A～J）のうち1人をフェアリーだと仮定してみましょう（フェアリーはピンクとします）。
Aがフェアリーだとすると、手を繋いでいるのは「ピクシーだ」とのことなので、BとJはピクシーであることがわかります（ピクシーはブルーにします）。
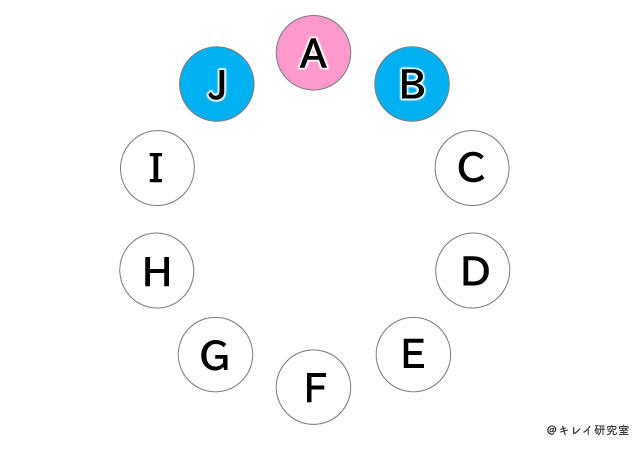
すると、Bが「ピクシーだ」と答えた相手（AとC）はフェアリーということになります。
続いて、フェアリーであるCが手を繋いでいる相手（BとD）はピクシーになります。
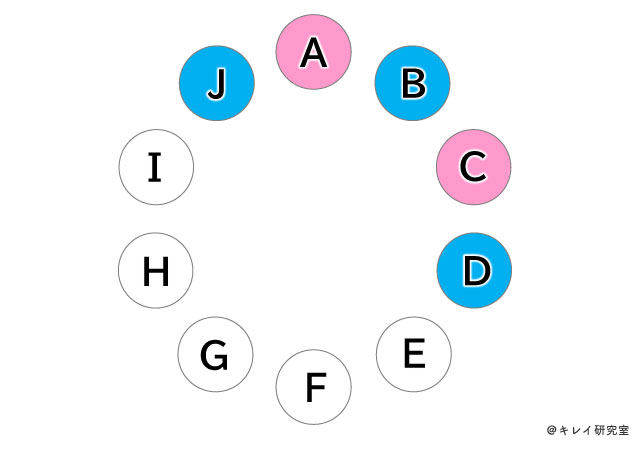
つまり、10人の妖精たちは、フェアリーとピクシーが交互に並んでいることになるのです。
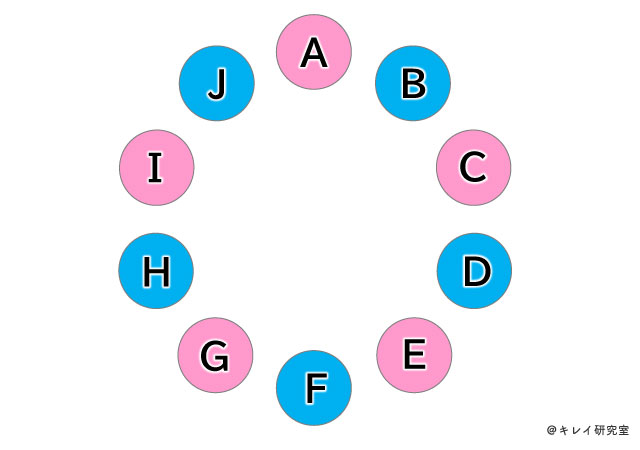
そのため、フェアリー・ピクシーともに5人ずつになりますね。
※最初にAをピクシーと仮定すると、BとJがフェアリーとなり、最終的に全てのフェアリーとピクシーが入れ替わりますが、交互に並んでいるのは同じなので、答えは同じになります。
答え：
5人
嘘つきと正直者を探す問題。
皆さまもクイズの本などで目にしたことがあると思います。
意外かもしれませんが、このようなパズルは数学として扱われ、受験などに出題されることも。
確かに、仮定をして、矛盾がないところまで導くという、論理的な思考に基づいた考えが数学的ですよね。
嘘つきパズルを解くポイントは、登場人物の1人を正直（もしくは嘘つき）と仮定して、場合分けしていき、矛盾が出ないパターンを探していくこと。
変化球としては、正直者（100％正直に答える）・嘘つき（100％噓をつく）に加え、普通の人（50％の確率で嘘をつく）が混ざることも。
この場合も、普通の人が嘘を答えた場合と正直に答えた場合というパターンを分けると、回答にたどり着けると思います。
複雑な問題は、パターン分けを表にまとめながら解くと、抜けが少なくなり、解きやすいですよ。
いかがでしたか？
疲れた脳にちょっと刺激を与え、リフレッシュする数学パズル。
楽しんでいただけるとうれしいです。
［執筆者］
船木 彩夏
化粧品メーカー研究員
［出演情報］
2023.12.2 TBSラジオ：井上貴博 土曜日の「あ」
＜資格＞
・サプリメントアドバイザー
・健康管理士一般指導員
・健康管理能力検定1級
［監修］キレイ研究室編集部
